线段树

什么是线段树？

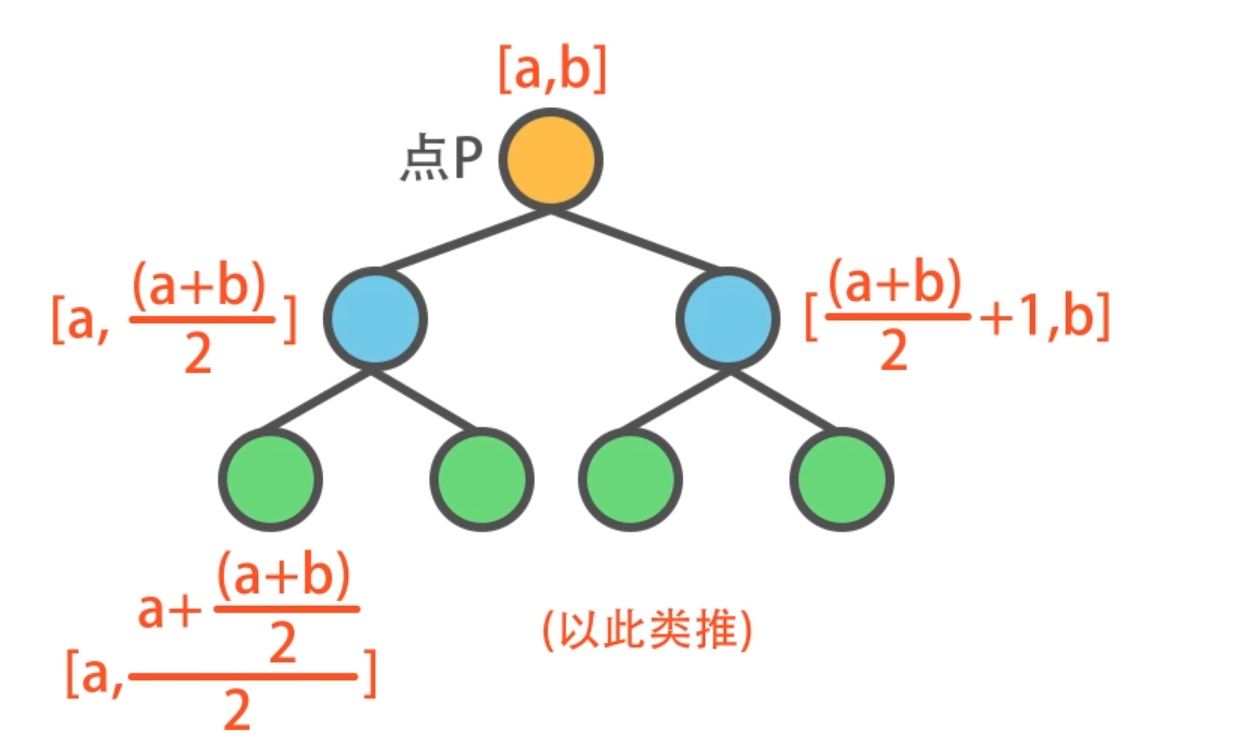
线段树是一种二叉树，广义上也被归类为二叉搜索树。它是一个工具，能将区间的修改、维护和查询，时间复杂度优化为log级别。

线段树的维护只需要小区间更新大区间，线段树是平衡二叉树。

线段树的使用局限性

问题需要满足：区间加法(对于[L,R]的区间，它的答案可以由[L,M]和[M+1,R]的答案合并求出) 。

满足的问题：区间求和，区间最大最小值等。

不满足的问题：区间的众数、区间最长连续问题、最长不下降问题等。

线段树解决问题的步骤

1. 建树

   • 以堆的方式存储数据

     graph TB;
     1((1))---2((2))
     1((1))---3((3))
     2((2))---4((4))
     2((2))---5((5))
     3((3))---6((6))
     3((3))---7((7))
     

     其中，若1号结点值为i，则其左子树结点值为2i，右子树结点值为2i+1，父结点值为i div 2(div为整除)。

   • 位运算计算效率更高

   • 线段树的数组一般要开到4*n才能防止出现越界访问

2. 单点修改

   • 当需要修改数列中下标为i的数据时，从根结点向下深度搜索，如果当前结点的左儿子的区间[L,R]包含了i，也就是L<=i<=R，就访问左儿子，否则就访问右儿子。直到L=R，也就是搜到了只包含这个数据的结点，就可以修改它。不要忘了将包含此数据的大区间的值更新。
   • 仅有单点修改的区间查询不需要处理lazy标记，步骤为：
     • 如果要查询的区间完全覆盖当前区间，直接返回当前区间的值；
     • 如果查询区间和左儿子有交集，搜索左儿子
     • 如果查询区间和右儿子有交集，就搜索右儿子
     • 最后合并处理两边查询的数据

3. 区间修改

   • 如果按照常规思路，向下递归遍历所有结点一一修改，时间复杂度和暴力处理相差无几。于是这里用到了lazy标记。
   • <lazy标记>将某个区间标记，表示这个区间的值已经更新，但它的子区间却没有更新，更新的信息就是标记里存的值。
   • 区间修改的步骤：
     • 如果要修改的区间完全覆盖当前区间，直接更新这个区间，打上lazy标记
     • 如果没有完全覆盖，且当前区间有lazy标记，先下传lazy标记到子区间，再清除当前区间的lazy标记
     • 如果修改区间和左儿子有交集，搜索左儿子
     • 如果修改区间和右儿子有交集，搜索右儿子
     • 最后将当前区间的值更新

4. 区间修改后的区间查询

   • 如果要查询的区间完全覆盖当前区间，直接返回当前区间的值
   • 如果没有被完全包含，下传lazy标记
   • 如果查询区间和左儿子有交集，搜索左儿子
   • 如果查询区间和右儿子有交集，搜索右儿子
   • 最后合并处理两边查询的数据

线段数模板例题

1. 已知一个数列，你需要进行下面两种操作：将某区间每一个数加上k，求出某区间所有数的和

   输入格式：

   第一行包含两个整数n, m(1<=n, m<=10^5)，分别表示该数列数字的个数和操作的总个数

   第二行包含n个用空格分隔的整数，其中第i个数字表示数列第i项的初始值

   接下来m行每行包含3或4个整数，表示一个操作：

   ​ 1 x y k：将区间[x, y]内的每个数加上k

   ​ 2 x y ： 输出区间[x, y]内每个数的和

   输出格式：

   输出包含若干行整数，即为所有操作2 的结果。

   输入：

   5 5

   1 5 4 2 3

   2 2 4

   1 2 3 2

   2 3 4

   1 1 5 1

   2 1 4

   输出：

   11

   8

   20